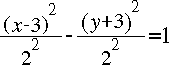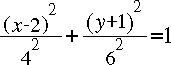A Student Assignment

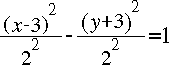
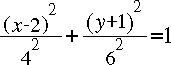
• determine the coordinates of all simultaneous solutions,
• determine the maximum distance between such solutions,
• estimate the slopes of the asymptotes, and
• submit an accurate drawing of the system.

1. Launch GrafEq by double-clicking its icon. Click on the title screen to remove it.
2. Enter the first relation above. Use the up key for the exponent and the slash (/) key for division.
3. Press Return to open a Create View window.
4. The default bounds (-10 to 10) are probably fine, so click on the Create button or press Return (which is equivalent to clicking on an outlined button).
5. Once the plotting is finished, your view window will appear as below:
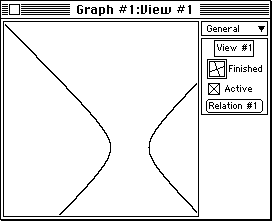
   Figure 1: a single relation, a hyperbola.
6. Under Graph, select New Relation by dragging and releasing the mouse.
7. Enter the second relation and then activate it by either pressing Return or clicking on the Active box. Your view window will show both relations. (See figure 2.)
   Figure 2: a simultaneous system, a hyperbola and an ellipse.
8. Press T to access the ticks side-bar and then click on its active box to display ticked axes. There are obviously simultaneous solutions in quadrants II, III and IV.
9. Press Z to access the zoom side-bar. Ensure that the Keep this view box is not checked. Position the cursor over the quadrant II solution, shrink the cursor box with the arrow keys and then option-click to zoom in to a View #2 window. Since you option-clicked, the View #1 window is retained—for subsequent access to the other solutions.
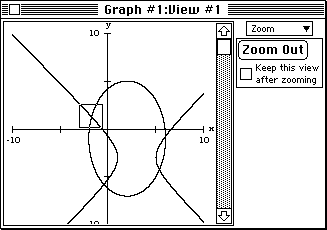
   Figure 3a: simultaneous system with zoom box positioned over a common point.
   
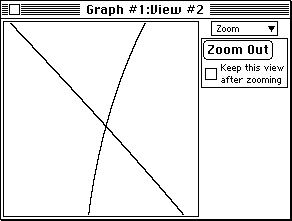
   Figure 3b: the view produced by zooming in.
10. Press 1 to access the one point side-bar and then place the cross hair cursor accurately on the intersection of the curves. The coordinates can be read from the side-bar. For better precision you may wish to zoom further in to this solution. If so, repeat from steps 9 and 10 on the second view but simply click—rather than option-click when zooming—since you will not wish to retain views. Once you are satisfied with the precision of the quadrant II solution, close all view windows except that for the first view, and repeat steps 9 and 10 for the other three solutions.
11. To determine the maximum distance separating solutions, first ensure that View #1 is active (foremost) and press 2 to access the two point side-bar. Place the cursor over one solution and press A, then over another solution and press B. The length of segment AB can be read directly from the side-bar (d, under Distance). The solutions furthest apart are as in figure 4a below.
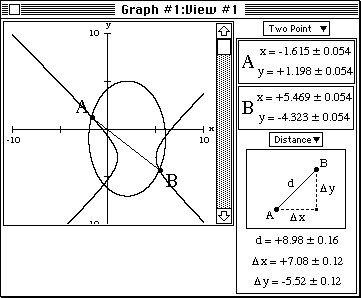
    Figure 4a: a segment AB that connects two solutions.
    
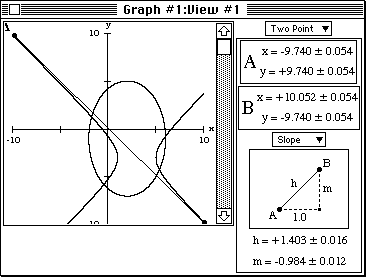
    Figure 4b: a segment AB that approximates an asymptote.
12. To approximate an asymptote, place A and B as far apart as possible as shown in figure 4b and select the slope mode in the side-bar. In this case the slope is near -1. By symmetry, the other asymptote will have slope 1. To confirm these values you can zoom out and re-evaluate the slope from points further apart.
13. To copy the graph accurately to paper:
    • Ensure that View #1 is foremost and press T to access the ticks side-bar.
    • Click on the lowest button in the simple display (dense ticks with crosses) and ensure the active box is checked.
    • You can now accurately copy the curves to graph paper.
    You can now terminate the GrafEq session by selecting Close Graph and then Quit under File.

The foregoing steps illustrate the graphics-based techniques appropriate to the modern secondary mathematics curriculum. An alternative method for determining the four solutions of the above system is as follows:

1. Enter both equations as separate constraints of a single relation as shown in figure 5a and plot this relation directly as shown in figure 5b.
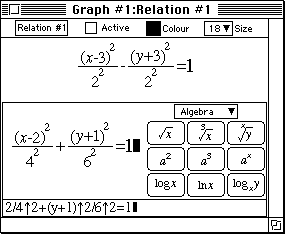
   Figure 5a: a single relation defined by two constraints.
   
   Figure 5b: solutions determined by plotting the formula of figure 5a.